扩散模型
引言
2020年的一篇论文,Denoising Diffsion Probabilistic Models 去噪扩散概率模型,本文的主要贡献在于
- 将扩散模型仅限于简单玩具数据集的理论概念中解放出来
- 更简单的生成目标
对于人脸的概率分布,其实压根就无法用一个概率分布p(x)来表示
扩散模型用一个看似不相关的流程来解决—从图像中去除高斯噪声
如果模型有效的话,那么它应当能够从随机噪声开始,逐步将其细化为有意义的图像
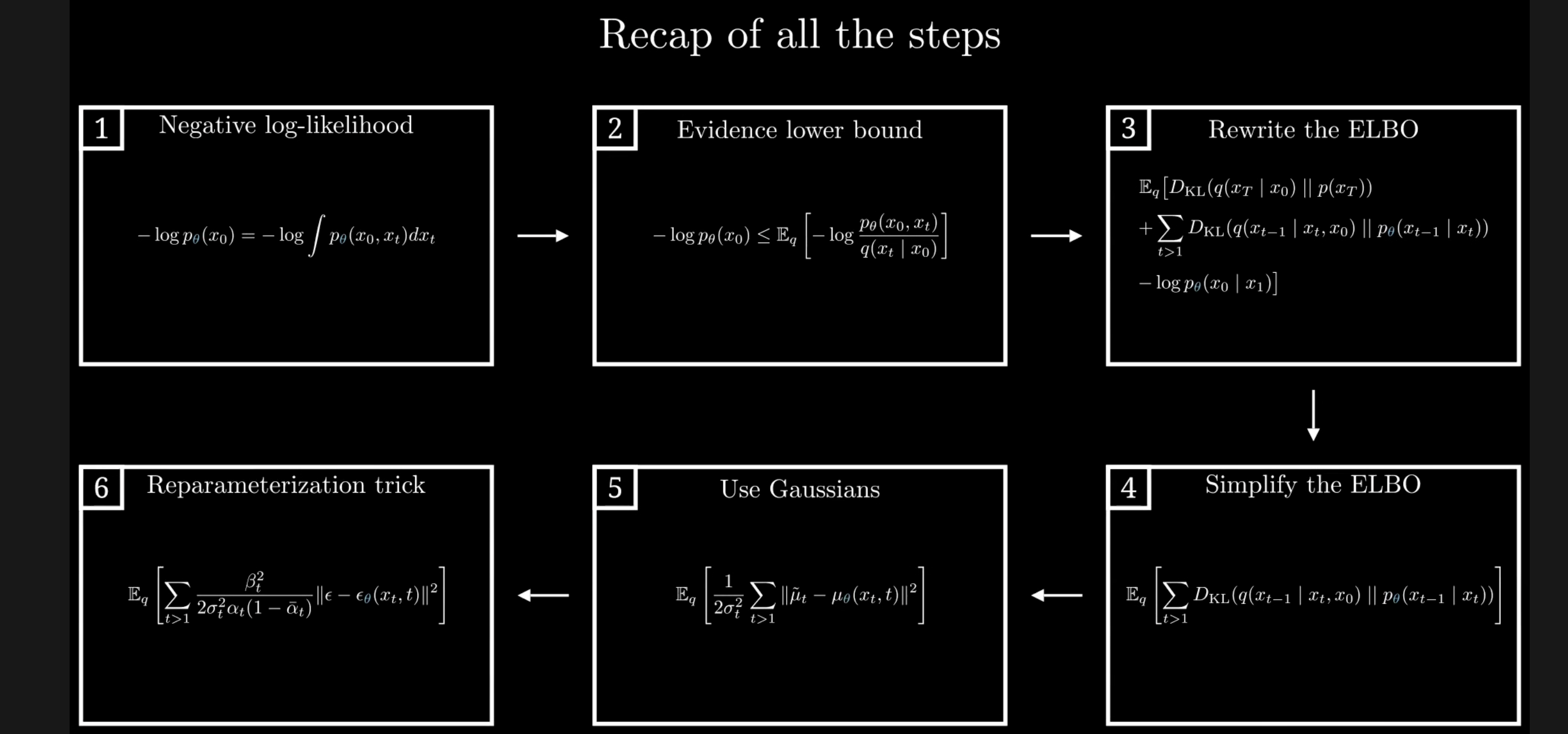
数学公式部分
前向过程
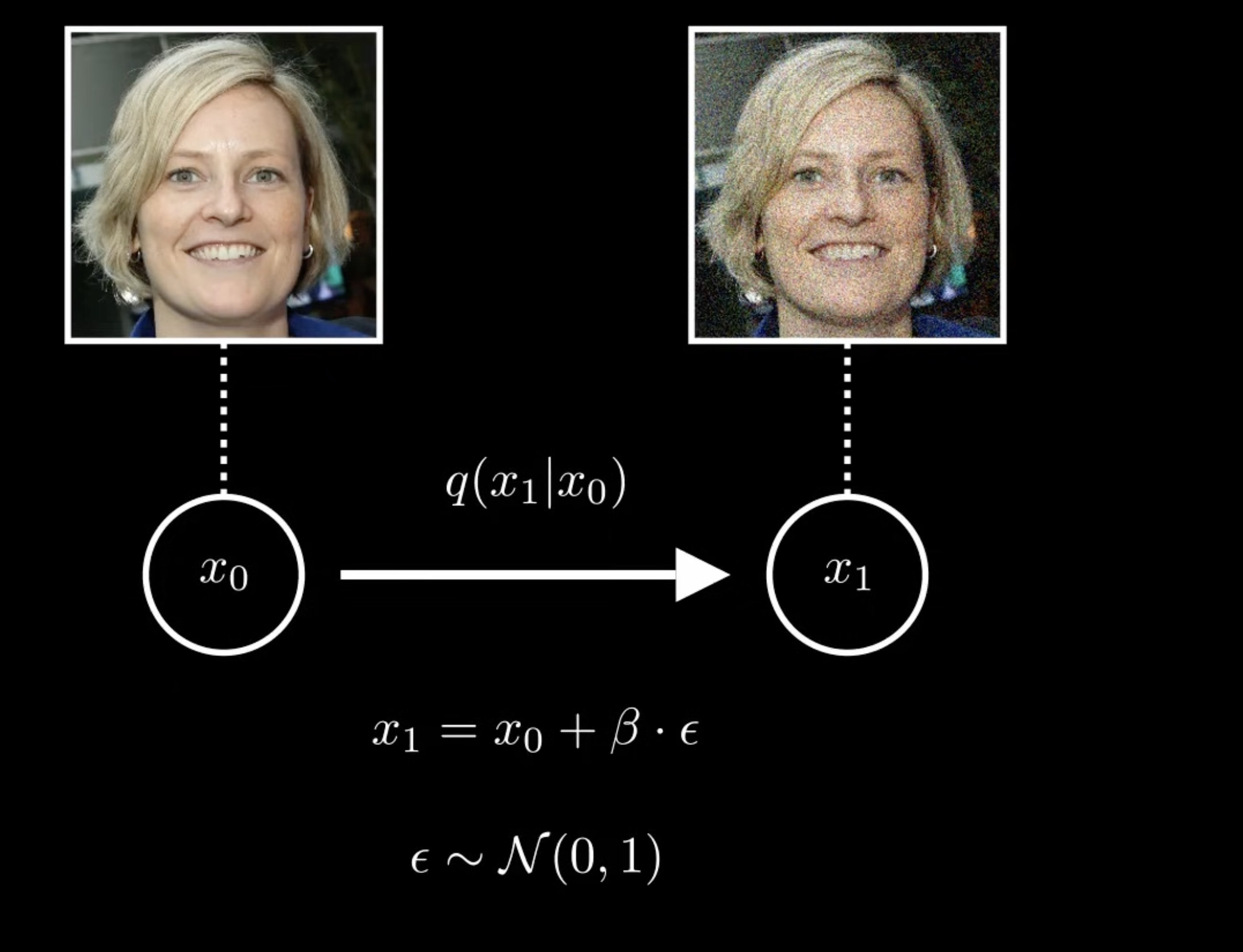
也就是说我们以 $x_0$ 为中心 方差为 $\beta$ 的高斯分布中抽取一个样本
不断重复这一个过程,那么就可以直接从 $x_0$ 到 $x_2$
同样的道理,在时间步长为t的情况下,也可以得到一个概率分布
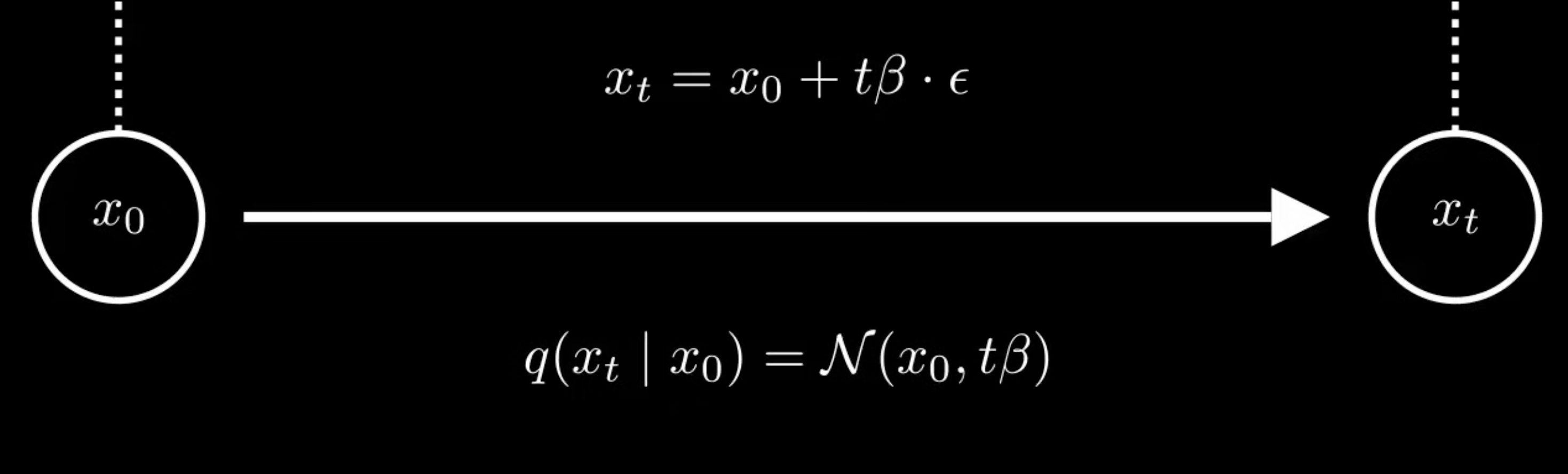
其中方差是 $t \cdot \beta$ 或 $\beta_t$
但是问题出现了,我们想要的分布的均值始终固定在 $x_0$,而方差无限的在增大
此时的我们的扩散过程绝对不会收敛于正态分布
这意味着我们需要重新设计我们的扩散过程
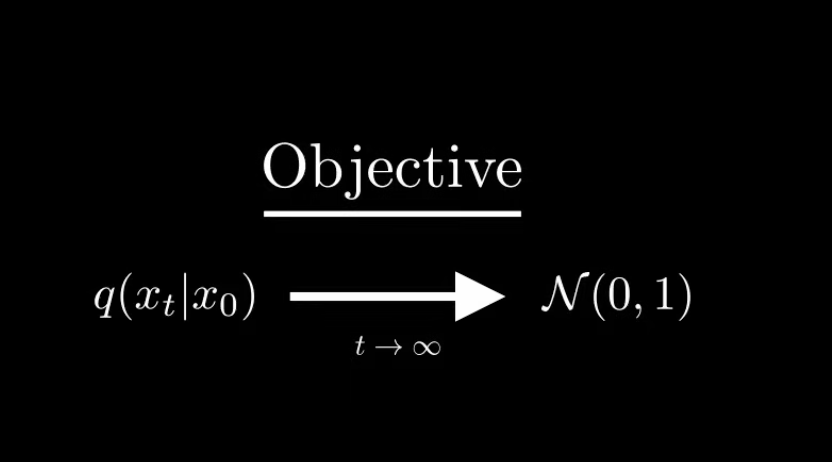
一个能将我们的数据变成标准正态分布的过程
- 均值必须收敛于0
- 方差收敛于1
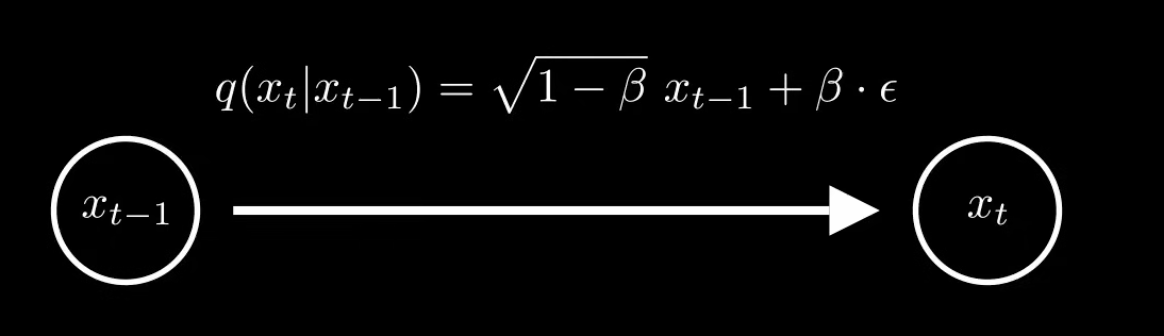
为什么选择 $\sqrt{1-\beta}$
DDPM的作者选择了这个系数,主要原因可能是简单性
当 $\beta \in [0,1]$ 时,$\sqrt{1-\beta} \in [0,1]$,这样可以确保均值逐渐收缩:$\mu_t = \sqrt{1-\beta_t} \cdot \mu_{t-1}$,同理方差也会趋近于1
这个公式可以让我们的原始数据分布变化为标准正态分布
实际上,扩散模型通常在每一步应用不同量的噪声,而非固定的 $\beta$ 值
因此现在我们定义了扩散的方法,它可以将我们的数据分布转换为标准正态分布
反向过程
我们首先从联合分布定义反向过程
$$p_\theta(x_{t-1}|x_t) = \mathcal{N}(x_{t-1}; \mu_\theta(x_t, t), \Sigma_\theta(x_t, t))$$
通过不断的累乘我们就可以得到x0的分布
所以我们需要做什么呢——让反向过程尽可能匹配前向的路径,这将通过最小化负对数似然来实现
但是积分下来几乎不可能,所以我们引入了一个ELBO下界
$$L = E_q[-\log p_\theta(x_0)] \leq E_q\left[\underbrace{D_{KL}(q(x_T|x_0)||p(x_T))}{L_T} + \sum{t>1}^T \underbrace{D_{KL}(q(x_{t-1}|x_t,x_0)||p_\theta(x_{t-1}|x_t))}{L{t-1}} + \underbrace{-\log p_\theta(x_0|x_1)}_{L_0}\right]$$